Romanowsky and Fall 2012 -- See the discussion of mass and angular momentum as the main parameters for galaxies, also the appendix for deprojection.
Friday, November 29, 2013
lit: Galaxies in LCDM with halo abundance matching
Trujillo-Gomez et al. 2011 -- Bolshoi resimulation also reproduces M-v_c relation.
Labels:
lcdm,
scaling relations,
simulations,
TF,
TFR,
todo,
writing
Thursday, November 28, 2013
lit: The Zeldovich approximation: key to understanding Cosmic Web complexity
Hidding, Shandarin et al. 2013: seems interesting, modelling the structure of the cosmic web.
Tuesday, November 26, 2013
Python: scikit-learn MoG
Probably should have tried this, before reinventing the wheel.
Sunday, November 24, 2013
lit: Verheijen et al, volume complete TFR, also declining rotation curves
see Verheijen et al. article on a volume-complete TF sample.
Also, the references therein, esp. Casertano & Van Gorkom, 1991 for a discussion of declining rotation curves in more massive galaxies.
Also, the references therein, esp. Casertano & Van Gorkom, 1991 for a discussion of declining rotation curves in more massive galaxies.
Thursday, November 21, 2013
lit: Velocity dispersions and dynamical masses for a large sample of quiescent galaxies at z>1
By Belli et al. They show that the stellar-dynamical mass ratio for massive ellipticals was in place at z > 1.
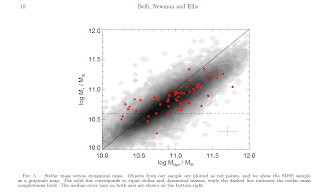
Wednesday, November 20, 2013
lit: Yegorova et al. 2007
A detailed investigation of the dependence of the slope of TFR on the radius where the velocity is measured. They find that the scatter is smallest at R = 0.6 R_opt (see fig.5).
Tuesday, November 19, 2013
lit: Some aspects of measurement error in linear regression of astronomical data, Kelly 2007
Kelly 2007:
I describe a Bayesian method to account for measurement errors in linear regression of astronomical data. The method allows for heteroscedastic and possibly correlated measurement errors and intrinsic scatter in the regression relationship. The method is based on deriving a likelihood function for the measured data, and I focus on the case when the intrinsic distribution of the independent variables can be approximated using a mixture of Gaussian functions. I generalize the method to incorporate multiple independent variables, non-detections, and selection effects (e.g., Malmquist bias).
I describe a Bayesian method to account for measurement errors in linear regression of astronomical data. The method allows for heteroscedastic and possibly correlated measurement errors and intrinsic scatter in the regression relationship. The method is based on deriving a likelihood function for the measured data, and I focus on the case when the intrinsic distribution of the independent variables can be approximated using a mixture of Gaussian functions. I generalize the method to incorporate multiple independent variables, non-detections, and selection effects (e.g., Malmquist bias).
LaTeX: \include vs. \input
I was annoyed by a page break that appears if I \include{a portion of my document}. Using \input{} instead solves this.
Monday, November 18, 2013
lit: Tonini et al. 2013, on physically meaningful radius for velocity measurements
They define the 'corrected' disk scale-length that includes the bulge potential. Pay attention to this article anyway -- they add a dynamical classificator dimension to the TFR, which is a little bit akin to what I'm doing.
Thursday, November 14, 2013
Daily paper: The Tully-Fisher relations of early-type spiral and S0 galaxies
I gave a talk at our group meeting yesterday, this was one of several useful suggestions and references I got.
bWilliams et al. 2010, The Tully-Fisher relations of early-type spiral and S0 galaxies
Offsets which are ascribed to fading or brightening could in fact be due to systematic biases that differ between the measures of rotation used. For typical slopes of the TFR, a relatively small systematic difference in velocity of ∼0.1 dex introduces an offset in the TFR that is indistinguishable from a ∼ 1mag difference in luminosity.
Our conclusions in this section have three consequences for previous works that measure the TFR of S0 galaxies using stellar kinematics corrected for asymmetric drift (e.g. Neistein et al. 1999; Hinz et al. 2001, 2003, BAM06): (i) the asymmetric drift correction they use yields similar results to detailed Jeans modelling; (ii) the drift correction does not seem to introduce a systematic bias between spirals and S0s and, if applied to samples of both spirals and S0s, can indeed be used to compare the TFRs of the two classes; (iii) however, a TFR derived from asymmetric drift-corrected stellar kinematics cannot be directly compared to TFRs derived from global HI line widths or resolved emission line PVDs. ==== There's a really interesting section on the ADC, and a nice comparison of gas/HI/AD corrected stellar kinematics. Also I should check their section on TFR fitting, intrinsic scatter in it, etc.In addition, I ought to take a look at the references therein, esp. the introduction.
Offsets which are ascribed to fading or brightening could in fact be due to systematic biases that differ between the measures of rotation used. For typical slopes of the TFR, a relatively small systematic difference in velocity of ∼0.1 dex introduces an offset in the TFR that is indistinguishable from a ∼ 1mag difference in luminosity.
Our conclusions in this section have three consequences for previous works that measure the TFR of S0 galaxies using stellar kinematics corrected for asymmetric drift (e.g. Neistein et al. 1999; Hinz et al. 2001, 2003, BAM06): (i) the asymmetric drift correction they use yields similar results to detailed Jeans modelling; (ii) the drift correction does not seem to introduce a systematic bias between spirals and S0s and, if applied to samples of both spirals and S0s, can indeed be used to compare the TFRs of the two classes; (iii) however, a TFR derived from asymmetric drift-corrected stellar kinematics cannot be directly compared to TFRs derived from global HI line widths or resolved emission line PVDs. ==== There's a really interesting section on the ADC, and a nice comparison of gas/HI/AD corrected stellar kinematics. Also I should check their section on TFR fitting, intrinsic scatter in it, etc.In addition, I ought to take a look at the references therein, esp. the introduction.
Tuesday, November 12, 2013
SQLITE: nested query for MoG
select avg(gc.r_mag) from luminosity_errors2 as gc where gc.califa_id in(select t.califa_id from tidal_influence as t where t.Ftop > -0 and t.Ftop <98)
Friday, November 8, 2013
Thursday, November 7, 2013
lit: TFR at z=2.2 with SINFONI IFU
Cresci et al. 2013 -- they also use genetic algorithms for velocity field modelling.
lit: The baryonic Tully–Fisher relation and galactic outflows
Dutton and van den Bosch 2009, also see Dutton et al. 2011.
lit: The baryonic Tully-Fisher relation and its implication for dark matter halos
Trachternach et al 2009: baryonic TFR as constraint of elongation of DM haloes.
lit: IFU observations of galaxies wrt TFR
Courteau 2003 is important: they observe 14 barred galaxies with Sparse Pak IFU in order to calibrate long-slit samples. To be discussed in talk/article!
lit: Skewness and kurtosis in BTFR
McGaugh 2012:
A persistent problem with interpreting astronomical data is whether Gaussian statistics actually apply. One reason for this is that systematic errors often dominate random ones. We can check whether this might be an issue here by examining higher order statistics like the skew (lopsidedness) and kurtosis (pointiness) of the distribution in the deviations perpendicular to the BTFR. If the data are well behaved (i.e., distributed normally), the skew and kurtosis should be small.
A persistent problem with interpreting astronomical data is whether Gaussian statistics actually apply. One reason for this is that systematic errors often dominate random ones. We can check whether this might be an issue here by examining higher order statistics like the skew (lopsidedness) and kurtosis (pointiness) of the distribution in the deviations perpendicular to the BTFR. If the data are well behaved (i.e., distributed normally), the skew and kurtosis should be small.
Monday, November 4, 2013
The difference between MCMC and simulations
from PSU astrostatistics lecture notes:
MCMC is a form of simulation, because MCMC generates random numbers and bases the inference on them. However, there are two important differences between MCMC and the simulation that we shall discuss here.
a) In MCMC we do not simulate from the target distribution directly. Instead, we simulate a Markov Chain that converges to the target distribution. Thus, MCMC performs approximate simulation.
b) The primary use of MCMC is in Bayesian statistics where we seek to simulate from the posterior distribution of the parameters. Classical simulation on the other hand simulates fresh data.
MCMC is a form of simulation, because MCMC generates random numbers and bases the inference on them. However, there are two important differences between MCMC and the simulation that we shall discuss here.
a) In MCMC we do not simulate from the target distribution directly. Instead, we simulate a Markov Chain that converges to the target distribution. Thus, MCMC performs approximate simulation.
b) The primary use of MCMC is in Bayesian statistics where we seek to simulate from the posterior distribution of the parameters. Classical simulation on the other hand simulates fresh data.
Subscribe to:
Comments (Atom)