It's easy to lie with histograms. Choosing a small histogram bin width brings out spurious peaks and you can claim to see signal while there are only random sampling fluctuations. Choosing a large histogram bin width lets you smooth over the data distribution, hiding peaks or gaps (see an example using the Cauchy distribution here). Choosing slightly different histogram widths for two distributions you are comparing can lead to wildly different histogram shapes, and thus to a conclusion the two datasets are not similar.
This problem was sitting at the back of my head for quite some time: we are making interesting claims about some property distributions in our sample, but to what extent are our histograms, i.e. data density distribution plots, robust? How can we claim the histograms represent the true structure (trends, peaks, etc) of the data distribution, while the binning is selected more or less arbitrarily? I think the data should determine how it is represented, not our preconceptions of its distribution and variance.
I tried to redo some of our histograms using Knuth's rule and astroML. Knuth's rule is a Bayesian procedure which creates a piecewise-constant model of data density (bluntly, a model of the histogram). Then the algorithm looks for the best balance between the likelihood of this model (which favours the larger number of bins) and the model prior probability, which punishes complexity (thus preferring a lower number of bins).
Conceptually, think of the bias-variance tradeoff: you can fit anything in the world with a polynomial of a sufficiently large degree, but there's big variance in your model, so its predictive power is negligible. Similarly, a flat line gives you zero variance, but is most probably not a correct representation of your data.
The histogram below, left shows our sample's redshift distribution histogram I found in our article draft. The right one was produced using the Knuth's rule. They might look quite similar, but the left one has many spurious peaks, while the larger bumps on the right one show the _real_ structure of our galaxies distribution in redshift space! The peak near 0.025 corresponds to the Coma galaxy cluster, while the peak at roughly 0.013 shows both the local large-scale structure (Hydra, maybe?) _and_ the abundance of smaller galaxies which do make it into our sample at lower redshifts.
Also consider this pair of histograms: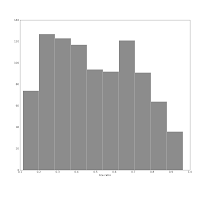
They show the axis ratio (b/a) of our sample of galaxies. The smaller this ratio is, the more inclined we assume the galaxy to be, with some caveats. The left one was produced using matplotlib's default bin number, which is 10, at least in Matlab after which matplotlib is modelled.I think are sqrt(n) or some other estimate.
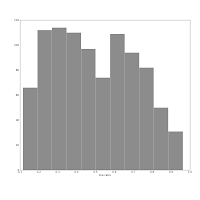
The right one shows the histogram produced using Knuth's rule. It shows the real data distribution structure: the downward trend starting at the left shows that we have more inclined, disk galaxies in our sample (which is true). The bump at the right, at b/a = 0.7, is the population of rounder elliptical galaxies. The superposition of these two populations is shown much more clearly in the second histogram, and we can make some statistical claims about it, instead of just trying to find a pattern and evaluate it visually. Which is good, because we the humans tend to find patterns everywhere and the noise in astronomical datasets is usually large.
This problem was sitting at the back of my head for quite some time: we are making interesting claims about some property distributions in our sample, but to what extent are our histograms, i.e. data density distribution plots, robust? How can we claim the histograms represent the true structure (trends, peaks, etc) of the data distribution, while the binning is selected more or less arbitrarily? I think the data should determine how it is represented, not our preconceptions of its distribution and variance.
I tried to redo some of our histograms using Knuth's rule and astroML. Knuth's rule is a Bayesian procedure which creates a piecewise-constant model of data density (bluntly, a model of the histogram). Then the algorithm looks for the best balance between the likelihood of this model (which favours the larger number of bins) and the model prior probability, which punishes complexity (thus preferring a lower number of bins).
Conceptually, think of the bias-variance tradeoff: you can fit anything in the world with a polynomial of a sufficiently large degree, but there's big variance in your model, so its predictive power is negligible. Similarly, a flat line gives you zero variance, but is most probably not a correct representation of your data.
The histogram below, left shows our sample's redshift distribution histogram I found in our article draft. The right one was produced using the Knuth's rule. They might look quite similar, but the left one has many spurious peaks, while the larger bumps on the right one show the _real_ structure of our galaxies distribution in redshift space! The peak near 0.025 corresponds to the Coma galaxy cluster, while the peak at roughly 0.013 shows both the local large-scale structure (Hydra, maybe?) _and_ the abundance of smaller galaxies which do make it into our sample at lower redshifts.
They show the axis ratio (b/a) of our sample of galaxies. The smaller this ratio is, the more inclined we assume the galaxy to be, with some caveats. The left one was produced using matplotlib's default bin number, which is 10, at least in Matlab after which matplotlib is modelled.The right one shows the histogram produced using Knuth's rule. It shows the real data distribution structure: the downward trend starting at the left shows that we have more inclined, disk galaxies in our sample (which is true). The bump at the right, at b/a = 0.7, is the population of rounder elliptical galaxies. The superposition of these two populations is shown much more clearly in the second histogram, and we can make some statistical claims about it, instead of just trying to find a pattern and evaluate it visually. Which is good, because we the humans tend to find patterns everywhere and the noise in astronomical datasets is usually large.
No comments:
Post a Comment