Daily Papers TODO: a collection of links

I'll be keeping the list of papers I want to read here.
Stellar Mass-to-Light Ratios and the Tully-Fisher Relation 3D Spectroscopy with VLT/GIRAFFE - IV: Angular Momentum and Dynamical Support of Intermediate Redshift Galaxies
ANGULAR MOMENTUM ACQUISITION IN GALAXY HALOS
The Baryonic TF relation -- we've discussed it before, but I need to write it up.

Daily Paper #10: Reconstructed density and velocity fields from the 2MASS Redshift Survey

Today's article was referenced to in the WISE TF paper I summarised yesterday. I wanted to find out how the peculiar velocities and density fields were reconstructed.
Title: Reconstructed density and velocity fields from the 2MASS Redshift Survey
Authors: Erdoğdu, Lahav et al.
Year: 2006, http://mnras.oxfordjournals.org/content/373/1/45.full
I have to admit I did not understand the mathematics of this article, and will read Peebles 1973 and Fisher 1995 to understand what are the spherical harmonics and Fourier-Bessel functions in detail. What they do in order to transform the the redshift space to the real space is decompose the redshift space distribution into radial and angular components. Peculiar velocities affect only the radial component, so it is easier to deconvolve them.
The relationship between mass and light distribution is usually assumed to be linear with some proportionality constant (there is an article by Vivienne arguing that this is not the case).
They provide density and velocity maps up to cz = 16 0000 km/s, which covers the CALIFA redshift range. I could ask them for the velocity data and obtain the peculiar velocities/infall corrected distances for the sample. I think it would be useful for me later, when working with the density fields and spin alignments. We would also have these distances and their errors for all the galaxies, not only the ones identified as belonging to structures.
Previously I used the Virgo-GA-Shapley infall corrected redshifts from NED (obtained using this model: http://iopscience.iop.org/0004-637X/529/2/786/fulltext/). It's a simpler model, taking only these three attractors into account.

Daily Paper #9: WISE TF: A Mid-infrared, 3.4-micron Extension of the Tully-Fisher Relation Using WISE Photometry

Here's the recent WISE paper my supervisor had sent me a link to.
Title:WISE TF: A Mid-infrared, 3.4-micron Extension of the Tully-Fisher Relation Using WISE Photometry
Authors: Lagattuta, Mould et al.
Year: 2013, http://arxiv.org/abs/1305.4637v1
In a way, this is a classic, straightforward observational TFR paper. They pick the shortest wavelength (3.4 um) WISE band, where dust emission is not very important, use archival HI linewidths from Hyperleda and Cornell HI archive and WISE photometry (w1gmag magnitudes). They also take morphological classifications from CfA ZCAT and axis ratios from V-band measurements in NED. They reject galaxies with low quality of radio observations and inclinations (from b/a) less than 45 deg, as well as all E galaxies.
What was interesting for me here was that they did a number of corrections in a thorough way, especially the peculiar velocities correction. Since their and CALIFA redshifts overlap, we might have to give more thought to this correction, as it can reduce scatter in the resulting TFR significantly. They use the Erdoglu 2006 model, interpolating over the velocity grid where necessary (I'll read it for tomorrow).
The intrinsic extinction correction are small in the mid IR, but not so in the SDSS r-band. I'll check Masters 2003 correction prescription too, maybe it's better than the one I'm using.
They also find a bend in their TFR, due to different morphological types -- like we do (the slopes for late and early spirals are different), which is worth mentioning! However, they normalise the magnitudes of the early types and force them to fit the late-type spirals relation. Since our sample is dominated by early-type spirals, I would not want to do that (and I'm not sure what physical basis there is for this correction).
There is a reference to a 2013 paper by Sorce et al., where it is claimed that redder galaxies lie above the TF relation, and the bluer ones lie below, that's interesting.
They also discuss the influence of a bulge to the scatter of TFR, which is larger at the IR and for massive galaxies -- I'll remember that.
What made me think is their conclusion that the mid-IR W1 and 2MASS K bands trace the same stellar populations, a significant fraction of which are in the central parts of the galaxies (thus, probably bulges, esp. in CALIFA sample). That is interesting, in part because we make the inclination and extinction corrections assuming the galaxies are thin disks. Also, we have to keep in mind that when we plot the TFR for different bands, we are relating disk rotation velocities with different morphological components of a galaxy, which do not necessarily correspond to the disk only!

Daily Paper #8: Constraints on the relationship between stellar mass and halo mass at low and high redshift

Title: Constraints on the relationship between stellar mass and halo mass at low and high redshift
Authors: Moster, Somerville et al.
Year: 2009, http://arxiv.org/abs/0903.4682
They give a nice breakdown of the methods used to link the halo properties with those of the galaxy. It is possible to obtain these relations from observations (kinematics, lensing, X-rays), from bottom-up modelling (N-body or SAMs), or by using a statistical approach: obtaining the probability that a halo with a certain mass hosts a certain number of galaxies with some certain properties (luminosity, type, etc.). This way, we don't have to make assumptions about feedback and other poorly-understood processes that plague the SAMs. I'll review the lecture recordings from Jerusalem School, I think the formalism used was explained in detail there.
The goal of this paper is to construct the conditional stellar mass function (as opposed to the conditional luminosity function). Such a function provides the average number of galaxies in a certain stellar mass range that reside in a halo with a mass M -- it can also be viewed as the stellar mass function for the haloes of mass M.
They use a N-body simulation to obtain a population of DM haloes and their merger tree information. The ratio of the halo mass M and the stellar mass M is not constant (due to different feedback processes), so they use a parameterisation of it to fill the haloes with galaxies, and obtain the stellar mass-Mhalo relation.
In order to obtain the conditional mass function, they divide the galaxies into centrals and satellites, parameterising their distribution in two different ways. The total CMF is the combination of the two.
They also obtain the M* -- M_halo relationship for higher redshifts, claiming that 'large halos accrete dark matter faster than large galaxies grow in stellar mass, while the growth of low mass halos is slower than that of the central galaxies they harbor', (see the attached picture).

This paper does not mention the TF relation, however, I wanted to find out more about the M*-Mhalo relation, the ways to determine it and its evolution. It's interesting that the high-mass end of this relation does not evolve much since z=4.

Daily Paper #7: Galaxy groups in the 2dFGRS: the number density of groups

Title: Galaxy groups in the 2dFGRS: the number density of groups
Authors: Eke, Baugh, Cole et al.
Year: 2006, http://adsabs.harvard.edu/abs/2006MNRAS.370.1147E
The authors determine the galaxy groups mass and luminosity functions from 2dFGRS Percolation-Inferred Galaxy Group (2PIGG) catalogue (getting about 29 000 groups). The catalogue and the mock catalogues used to determine and correct for bias are described in Eke 2004 paper.
They obtain dynamical masses of the clusters (I think they use the words 'cluster' and 'group' interchangeably here) from their velocity dispersions, and obtain their luminosities by simply adding up the members' luminosities with weighting to account for spectroscopic incompleteness and galaxies below the flux limit. Then they correct the mass and luminosity functions using the Vmax method. However, they claim that a more robust way to determine the group mass function is deriving it from the luminosity function by multiplying it by a mass-to-light ratio. They also show that the total group luminosity function depends on the group finding algorithm used.
The main goal of the article is to determine the \sigma_8 parameter, but they make a comparison between halo velocities and circular velocities, claiming that the two are similar. The authors claim it is possible to convert a halo luminosity to its circular rotation velocity directly, then convert group luminosities (which are very similar to those of the brightest galaxy of the group) to circular velocities using Bell & de Jong B-band TF relation, and compare the two (see the attached figure).


I think it is an important article, because it is observational, and worth citing while discussing the halo/galaxy velocities issue (the ratio of v_c/v_200 is around 1.2, at least from the simulations, not close to 1 as they find here). Anyway, I'll remember this article in case I have enough time to work on the velocity function.

Daily Paper #6: A physical model of cosmological simulations of galaxy formation

I picked this article for the group meeting presentation, and actually read it, because it is rather relevant.
Title: A physical model of cosmological simulations of galaxy formation
Authors: Vogelsberger, Genel, Sijacki et al.
Year: 2012, http://arxiv.org/pdf/1305.2913v1.pdf
They present galaxy formation simulations using the AREPO code, which is a moving mesh hydro code, claimed to combine the advantages of SPH and semi-analytical models built on top of N-body simulations. What is important, however, is that they include, among other things:
-- BH seeding and growth
-- 3 modes of AGN feedback (thermal, kinetic (radio jets) and EM radiation). The discrepancy between the high-mass end of McCarthy, Schaye et al. TFR and observations I discussed yesterday is probably due to lack of AGN feedback prescriptions.
-- realistic cooling (including metals) with self-shielding
-- realistic enrichment timescales and yields
-- different modes of outflows

The article itself is quite long and rather technical, dealing with the details of the implementation of physics. However, there are some interesting observations. For instance, they discuss the stellar mass function and its relation to feedback, halo mass function and the cosmic SFH. The stellar mass function is 'chewed' by stellar feedback (SN and stellar winds) at the low halo mass end, and by AGN feedback at the higher mass end. It can be viewed as the convolution of the halo mass function with the efficiency with which stars form in these haloes (i.e. feedback mechanisms).

I think this relation is really important -- actually, it shows why the TFR exists, and why there is a knee at the high-mass end. _Why_ the slope, zeropoint and scatter are such are different questions -- but the answer to that should be some combination of the halo concentration (i.e. response to baryons, mostly), details of feedback (which determine the shape of the M* -- Mhalo relation) and the initial halo mass function (i.e. cosmology). The latter also sets the angular momentum of galaxies (Vvir -- Mvir are related, see the description of Dutton 2011).

They reproduce the stellar mass-halo relation, stellar mass function, evolution of the cosmic SFR density, the cosmic stellar mass density, mass-metallicity relation, SDSS luminosity function, M_BH -- M* relation and the Tully-Fisher relation (in the Vcirc -- M* sense, see the other attached plot). They claim (by citing McCarthy & Schaye, and experimenting with different radii) that the precise radius of the velocity measurement is not very important.

They conclude that TFR is not very sensitive to feedback parameters (shown in the plot). However, feedback must be included, otherwise it is not possible to reproduce TFR correctly. They find that the stellar mass in a halo is primarily set by the stellar feedback and radio-mode AGN feedback.

Todo: Eulerian vs. Lagrangian

Do you go with the flow, or stay in a fixed point in space?

Daily Paper #4: Dark halo response and the stellar initial mass function in early-type and late-type galaxies

Our group meeting ate most of my day, so here's a delayed review. Title: Dark halo response and the stellar initial mass function in early-type and late-type galaxies
Authors: Dutton, Conroy, van den Bosch et al., http://arxiv.org/abs/1012.5859
Year: 2011
The authors try to find the origins of the TF and Faber-Jackson relations, using a big sample of observed galaxies from SDSS, a set of observational scaling relations showing the distribution of baryons in galaxies, with constrains on the DM halo structure from simulations.
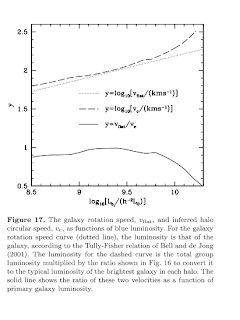
They claim in the introduction that the origin of TFR and FJR is the relation between the halo virial velocity and its virial mass, which scales as v_vir \propto M^(1/3). The relation between v_opt (*) and v_vir depends on 3 factors:
-- the contribution of baryons to v_opt
-- the structure of pristine (DM-only) haloes. The halo profiles are well-enough defined by the NFW profile.
-- and the halo response to the disk formation (contraction/expansion)
The biggest source of uncertainty for the first factor is the IMF, as most of the baryonic mass in galaxies (except the low-mass star-forming ones) is in stars.
The third factor, the halo response, is quite uncertain. It can be adiabatic or non-adiabatic contraction, or expansion due to a number of different processes.
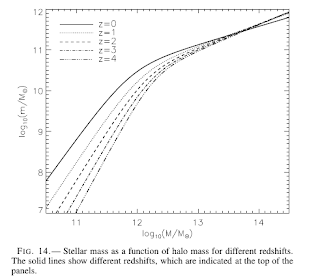
They use a large number of observed relations (TF and FJ relations too) to constrain or predict unknown quantities in their analytic model, modelling the DM halo, bulges, disks, gas disks, constructing 3D models of their SDSS sample galaxies (~100 000 LTGs, ~160 000 ETGs).
They construct mass models for all those galaxies using various IMF and assumptions about the halo response. Then they compare them with the observed circular velocity -- stellar mass relations (I do not understand it at this point -- they already used the TFR as a constraint while solving for the halo contraction at a given IMF, so it is inbuilt in their model somehow?).
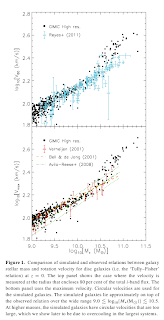
Nevertheless, they do not reproduce the zero-point of the TFR with the standard Chabrier IMF and standard adiabatic halo contraction model, as the velocity is overpredicted. They claim that it is possible to fix that by either assuming a different IMF, or changing the halo response, or having different halo concentrations (set by formation time or \sigma_8, they claim that both ways to do it do not solve the zero-point problem).
However, they find that early-type and late-type galaxies cannot have the same IMF and halo response. For any given halo response model, ETGs and LTGs must have different IMF normalisations to reproduce the TFR. If we assume a universal IMF, early-type galaxies require stronger halo contraction.
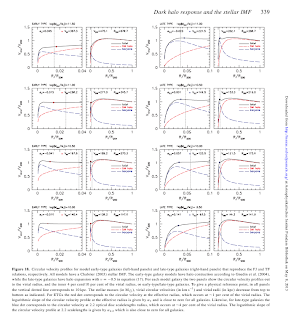
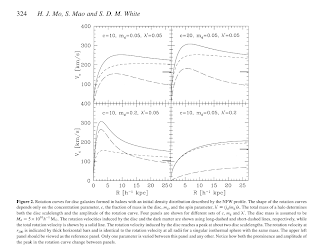
They look into the model circular velocity profiles (see attached) for models that reproduce the TF and FJRs, with Chabrier IMF. The velocity profiles look rather constant at higher radii, reaching the maximum at ~0.3 R_vir. (For the LTGs, they convert the velocity dispersion to v_circ picking a rather simple conversion factor between sqrt(2) and sqrt(3).) They claim that the flatness of the rotation curves does not depend strongly on the IMF and the halo response model, and 'is a natural consequence for galaxies embedded in LCDM haloes'.
Then they discuss possible mechanisms that would account for differences in IMF or halo response for ETGs and LTGs. The halo contraction/expansion may depend on galaxy morphology via a number of processes:
-- adiabatic contraction due to smooth accretion -- results in disk growth and SF, important for LTGs
-- wet major mergers -- result in halo contraction because gas settles in the center of a galaxy, transforms LTGs to ellipticals
-- dry major mergers ( for ETGs) -- halo contraction due to violent relaxation which mixes stars and DM
-- clumpy accretion/minor mergers: halo expansion due to dynamical friction. Clumps must be baryonic, so that's likely to occur at high redshifts (A. Dekel was arguing in Jerusalem that it must be the case).
-- feedback causes halo expansion, more important to LTGs and for higher redshifts.
-- bars -- halo expansion or contraction, not clear.

They sum it all up by saying that the key formation event that distinguishes ETGs from LTGs is a major merger (dry or wet), which causes halo contraction. For LTGs, haloes could expand due to a combination of clumpy cold accretion and intensive feedback.
The IMF may plausibly vary with redshift due to its alleged dependence on ISM temperature via the Jeans mass. Since ETGs form their stars earlier than LTGs, their IMF might be different. They discuss the van Dokkum & Conroy 2008 article on the different IMF at the cores of massive ellipticals, and conclude that this IMF would not fit for the other ETGs well.
All in all, they show that there is a degeneracy between IMF and the halo response to disk formation, and we cannot match the two for ETGs and LTGs if we want to reproduce the TFR. However, I'm puzzled here -- like in the previous Mo, Mao, White article, they do not model galaxy evolution in a self-contained way, and a model cannot show things that are not included in it. Mo, Mao & White include one set of parameters in their article, and get a set dependences on their parameters (like the disk formation time). Here Dutton et al. model rotation curves as functions of other parameters, and get dependence on another set of parameters. I think it's tricky to understand which parameters are really important, because in astrophysics we often have many coupled parameters, and it's not difficult to find correlations between them. It's more difficult to find out which ones are the fundamental ones, which really affect the TFR.
-- a question: what does it mean "TFR is an edge-on projection of the fundamental plane" (p. 323)?
(*) v2.2 for late-type galaxies and some measure of velocity proportional to dispersion at the effective radius for early types

Daily Paper #3: Rotation rates, sizes and star formation efficiencies of a representative population of simulated disc galaxies

I was a bit late today, because I went to see a couple of talks at the HETDEX meeting. A couple of interesting points from there:
-- The LAE people are worried about selection bias arising due to galaxy spins' alignment with the large scale structure (http://arxiv.org/abs/1004.3611)
-- Cluster growth depends not only on the proto-cluster environment (i.e. the immediate neighbourhood), but on super-halo scales as well (it's probably better defined here: http://arxiv.org/abs/1109.6328)

...On to the paper:
Title: Rotation rates, sizes and star formation efficiencies of a representative population of simulated disc galaxies
Authors: McCarthy, Schaye et al.
Year: 2012, http://arxiv.org/abs/1204.5195 They use resimulated (SPH) Millenium sub-regions with selected representative mean densities, including baryonic physics. They include background UV/Xray radiation field that 'reionises' the simulations at z = 9 and the CMB. They model star formation using an effective prescription reproducing the Kennicut's relation and assuming Chabrier IMF, as well as yields and timing of nucleosynthesis and SN feedback.
Then they fit the surface brightness profiles of galaxies in 9 - 11.5 log M* range with a Sersic function and classify their galaxies into disc and spheroid-dominated usin n = 2.5 as the cut.
-- The stellar mass - rotation velocity relation:
They examine this relation for their disk galaxy population (see the attached picture) and compare it with Reyes 2011 observations, claiming that this is the first cosmological hydrodynamical simulation that produces a population of galaxies consistent with the observed TFR. The slope is slightly higher, but in general, the agreement is really good. They use v80 (velocity at 80% light radius) and Vmax as the velocity measures. The velocities at their high-mass range are too big, and they claim that lack of prescription for AGN feedback may explain that.
The authors also discuss the scatter in TF relation, claiming that it is not possible to directly compare observed and simulated TF scatter without careful analysis of selection criteria and observational uncertainties.
Simulated spheroid galaxies follow the TFR well at this mass range, except for the most massive galaxies. The rotation curves of the galaxies with M* > 10.6 are not realistic (due to overcooling, too efficient SF of the highest mass haloes). Their simulated galaxies are also compatible with observed M* - size and star formation efficiency -- M* relations, up to the higher mass range.
One more quantity that simulations are compared with is the ratio of v_circ to v_200. If there is no significant halo expansion/contraction, this ratio should be roughly equal to 1.2 (Duffy 2010 writes more on halo expansion/contraction issue and impact on this ratio). Again, their results agree with this quite well up to log(M*) > 10.5.
They try to reproduce the main galaxy sequence at z = 0, comparing their results with SFR from Galex. Except for the lowest mass galaxies where their resolution is too small, it works well.
The section 4 is an interesting discussion of connection between SF efficiency, stellar mass function and the TF relation. They show that by assuming power-law shapes for halo mass function and stellar mass function in certain stellar mass range where this is valid, it is possible to match haloes (=velocities) and stellar masses using the abundance matching method, and reproduce TFR and SFR efficiency-M200 relations well (and maybe even constrain the faint end of the IMF). The way I understand it, the TFR arises due to the linear (in log-space) match between the halo mass function (set by cosmology) and the stellar mass function (set by IMF, SFR efficiency, thus feedback, etc.). I'll read Mo, van den Bosch and White 2010 for more discussion on this matter.

Daily Paper #2: The Tully-Fisher Zero Point Problem

Today's is a short paper (conference proceedings, just 4 or so pages), dealing with the halo contraction/expansion issue.

Title: The Tully-Fisher Zero Point Problem
Authors: Dutton, van den Bosch & Courteau
Year: 2008, http://arxiv.org/abs/0801.1505

The authors claim that CDM-based disk formation models can reproduce the slope/scatter of the TFR, however, its zeropoint has not been matched. This problem gets even worse if additional constraints (disk sizes, number densities) are imposed.
The TFR zeropoint can be matched in models if the halo contraction or disk self-gravity are not taken into account, or, as is shown in the article, halo contraction is counteracted by baryon feedback. They model an exponential disk in a NFW halo, obtain its luminosity from observed TFR and its scale-length from the size-luminosity relation. Assuming WMAP3 cosmology and a concentration parameter value from simulations, they solve for the virial mass and obtain rotation curves with and without the halo contraction (see the attached plot). The halo-contraction case is in conflict with both theory and observations, meaning that the halo is too small and has too high spin parameter.
They suggest 3 ways to solve this problem:

• -- lower the stellar mass-to-light ratio (but there is no known IMF that could provide that). Also, they claim that baryons at the disk and bulge account for at least half of the v2.2 -- I didn't know that (Courteau 1999, Weiner 2001)!
• -- lower the initial concentration (then the virial radius of a halo is increased) -- but that's incompatible with WMAP3 cosmology.
• -- turn off or reverse halo contraction: disk galaxies do not form in isolated haloes by smooth cooling. Halo contraction can be reversed by:
  • a) Feedback during adiabatic disk formation, if a large fraction of its mass is removed. It would also explain why galaxy formation is so inefficient (I think they mean that the gas is not converted into stars rapidly).
  • b) Dynamic friction between baryons and DM due to bars or large baryonic clumps (do they mean violent disk instabilities here?). They do not explain the details of such a process here, but I think what happens is that baryons transfer some of their angular momentum to the halo due to formation of massive, concentrated, rapidly moving structures.

The interesting message of the article is that the TFR zeropoint can provide clues into baryon feedback (which should also explain the core-cusp problem of DM haloes, at least that was what A. Dekel and J. Primack maintained at the Jerusalem Winter School). That's important.

Daily Paper: The formation of galactic discs

Me and my supervisor agreed that I would read a paper a day and write it up, so I'll be copying the summaries here.

Title: The formation of galactic discs (http://adsabs.harvard.edu/abs/1998MNRAS.295..319M)
Authors: Mo, Mao, White
Year: 1998
It's actually a really important paper -- I'm glad not to have missed it. They model galactic disk formation (of pure exponential ones, though they address influence of a simple bulge model later) in 3 CDM cosmologies. The authors make 4 important assumptions:
1) The mass of a disk is a fixed fraction of its halo
2) The angular momentum of the disk is also a fixed fraction of that of the DM halo (later they find that the specific angular momenta of the disk and halo are similar, so these two ratios should be equal).
3) The disk is thin, has an exponential density profile and is centrifugally supported
4) Real galaxies are dynamically stable disks, i.e. they reject unstable models.

They calculate the halo mass function using Press-Schechter formalism (see Appendix), assume halo angular momentum distribution determined by N-body simulations and a constant mass-to light ratio, and NFW profile. They calculate the total energy of a truncated (to r_200) NFW halo using the virial theorem, the rotation curve corresponding to it (after accounting for adiabatic halo contraction and gravitational disk influence).
See the attached picture (Mo1998_rotcurves.png) for their results. They claim that the shape of a rotation curve depends on 3 parameters only: the halo concentration parameter c(see *), fraction of mass in the disk m_d, and the spin parameter.

There is a lot more in this paper, but they devote a significant section of it to Tully-Fisher relation, explaining the origins of its slope, zeropoint and intrinsic scatter.

• -- slope: They claim that it is a generic prediction of hierarchical structure formation models with CDM-like fluctuation spectra (which set the halo formation times and thus their concentration c distribution).
• -- zeropoint: mostly set on disk mass fraction, mass-to-light radio and the redshift at which a given disk was assembled. They claim that disks must have effectively formed at redshifts close to zero (?), unless we assume an unphysical mass-to-light ratio.
• -- scatter: they analyse possible sources of intrinsic scatter of the disks, and find that:
  • --- a small amount of scatter comes from the spin parameter distribution
  • --- scatter in concentration c also adds scatter to the TF relation (disks at more concentrated haloes spin faster).
  • --- bulge is not included in their model, so bulge luminosity contribution is not accounted for -- that's a source of scatter as well
  • --- mass-to-light ratio may vary, adding some more scatter
  • --- formation times may vary as well, adding even more scatter.

The intrinsic scatter because of the first two factors cannot be smaller than 0.15 mag.
In conclusion, they show that it is possible to derive a realistic TF relation theoretically, however, I'm not sure if that is the only way it could arise? They do not include bulges, which are important for our sample, too. I am also unsure what do they mean with 'effective disk assembly redshift' at z <= 1.

* c == r_200/r_s, here r_200 -- the limiting radius of a halo, defined so that the mean density inside this radius is 200 times larger than the background density, r_s -- the disk scale length.
There is also a brief explanation of the \sigma_8 parameter -- see attached.

lit: Non-linear structure formation

Slides from F. van den Bosch, from a talk given at Jerusalem Winter School.
A Gaussian random field is completely specified by either the two-point correlation function ξ(r), or, equivalently, the power spectrum P(k)

lit: Halo assembly bias

slides by F. van den Bosch.

lit: Baryonic T-F relation

S. McGaugh et al, somehow the baryons know how many stars to form'.
There is also a reference to Mo 1998, which may provide insights into the origin of the T-F relation.