Daily Paper #3: Rotation rates, sizes and star formation efficiencies of a representative population of simulated disc galaxies

I was a bit late today, because I went to see a couple of talks at the HETDEX meeting. A couple of interesting points from there:
-- The LAE people are worried about selection bias arising due to galaxy spins' alignment with the large scale structure (http://arxiv.org/abs/1004.3611)
-- Cluster growth depends not only on the proto-cluster environment (i.e. the immediate neighbourhood), but on super-halo scales as well (it's probably better defined here: http://arxiv.org/abs/1109.6328)

...On to the paper:
Title: Rotation rates, sizes and star formation efficiencies of a representative population of simulated disc galaxies
Authors: McCarthy, Schaye et al.
Year: 2012, http://arxiv.org/abs/1204.5195 They use resimulated (SPH) Millenium sub-regions with selected representative mean densities, including baryonic physics. They include background UV/Xray radiation field that 'reionises' the simulations at z = 9 and the CMB. They model star formation using an effective prescription reproducing the Kennicut's relation and assuming Chabrier IMF, as well as yields and timing of nucleosynthesis and SN feedback.
Then they fit the surface brightness profiles of galaxies in 9 - 11.5 log M* range with a Sersic function and classify their galaxies into disc and spheroid-dominated usin n = 2.5 as the cut.
-- The stellar mass - rotation velocity relation:
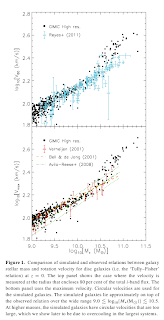They examine this relation for their disk galaxy population (see the attached picture) and compare it with Reyes 2011 observations, claiming that this is the first cosmological hydrodynamical simulation that produces a population of galaxies consistent with the observed TFR. The slope is slightly higher, but in general, the agreement is really good. They use v80 (velocity at 80% light radius) and Vmax as the velocity measures. The velocities at their high-mass range are too big, and they claim that lack of prescription for AGN feedback may explain that.
The authors also discuss the scatter in TF relation, claiming that it is not possible to directly compare observed and simulated TF scatter without careful analysis of selection criteria and observational uncertainties.
Simulated spheroid galaxies follow the TFR well at this mass range, except for the most massive galaxies. The rotation curves of the galaxies with M* > 10.6 are not realistic (due to overcooling, too efficient SF of the highest mass haloes). Their simulated galaxies are also compatible with observed M* - size and star formation efficiency -- M* relations, up to the higher mass range.
One more quantity that simulations are compared with is the ratio of v_circ to v_200. If there is no significant halo expansion/contraction, this ratio should be roughly equal to 1.2 (Duffy 2010 writes more on halo expansion/contraction issue and impact on this ratio). Again, their results agree with this quite well up to log(M*) > 10.5.
They try to reproduce the main galaxy sequence at z = 0, comparing their results with SFR from Galex. Except for the lowest mass galaxies where their resolution is too small, it works well.
The section 4 is an interesting discussion of connection between SF efficiency, stellar mass function and the TF relation. They show that by assuming power-law shapes for halo mass function and stellar mass function in certain stellar mass range where this is valid, it is possible to match haloes (=velocities) and stellar masses using the abundance matching method, and reproduce TFR and SFR efficiency-M200 relations well (and maybe even constrain the faint end of the IMF). The way I understand it, the TFR arises due to the linear (in log-space) match between the halo mass function (set by cosmology) and the stellar mass function (set by IMF, SFR efficiency, thus feedback, etc.). I'll read Mo, van den Bosch and White 2010 for more discussion on this matter.