Me and my supervisor agreed that I would read a paper a day and write it up, so I'll be copying the summaries here.
Title: The formation of galactic discs (http://adsabs.harvard.edu/abs/1998MNRAS.295..319M)
Authors: Mo, Mao, White
Year: 1998
It's actually a really important paper -- I'm glad not to have missed it. They model galactic disk formation (of pure exponential ones, though they address influence of a simple bulge model later) in 3 CDM cosmologies. The authors make 4 important assumptions:
1) The mass of a disk is a fixed fraction of its halo
2) The angular momentum of the disk is also a fixed fraction of that of the DM halo (later they find that the specific angular momenta of the disk and halo are similar, so these two ratios should be equal).
3) The disk is thin, has an exponential density profile and is centrifugally supported
4) Real galaxies are dynamically stable disks, i.e. they reject unstable models.
They calculate the halo mass function using Press-Schechter formalism (see Appendix), assume halo angular momentum distribution determined by N-body simulations and a constant mass-to light ratio, and NFW profile. They calculate the total energy of a truncated (to r_200) NFW halo using the virial theorem, the rotation curve corresponding to it (after accounting for adiabatic halo contraction and gravitational disk influence).
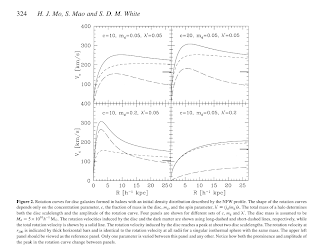
See the attached picture (Mo1998_rotcurves.png) for their results. They claim that the shape of a rotation curve depends on 3 parameters only: the halo concentration parameter c(see *), fraction of mass in the disk m_d, and the spin parameter.
There is a lot more in this paper, but they devote a significant section of it to Tully-Fisher relation, explaining the origins of its slope, zeropoint and intrinsic scatter.
The intrinsic scatter because of the first two factors cannot be smaller than 0.15 mag.
In conclusion, they show that it is possible to derive a realistic TF relation theoretically, however, I'm not sure if that is the only way it could arise? They do not include bulges, which are important for our sample, too. I am also unsure what do they mean with 'effective disk assembly redshift' at z <= 1.
* c == r_200/r_s, here r_200 -- the limiting radius of a halo, defined so that the mean density inside this radius is 200 times larger than the background density, r_s -- the disk scale length.
There is also a brief explanation of the \sigma_8 parameter -- see attached.

Title: The formation of galactic discs (http://adsabs.harvard.edu/abs/1998MNRAS.295..319M)
Authors: Mo, Mao, White
Year: 1998
It's actually a really important paper -- I'm glad not to have missed it. They model galactic disk formation (of pure exponential ones, though they address influence of a simple bulge model later) in 3 CDM cosmologies. The authors make 4 important assumptions:
1) The mass of a disk is a fixed fraction of its halo
2) The angular momentum of the disk is also a fixed fraction of that of the DM halo (later they find that the specific angular momenta of the disk and halo are similar, so these two ratios should be equal).
3) The disk is thin, has an exponential density profile and is centrifugally supported
4) Real galaxies are dynamically stable disks, i.e. they reject unstable models.
They calculate the halo mass function using Press-Schechter formalism (see Appendix), assume halo angular momentum distribution determined by N-body simulations and a constant mass-to light ratio, and NFW profile. They calculate the total energy of a truncated (to r_200) NFW halo using the virial theorem, the rotation curve corresponding to it (after accounting for adiabatic halo contraction and gravitational disk influence).
See the attached picture (Mo1998_rotcurves.png) for their results. They claim that the shape of a rotation curve depends on 3 parameters only: the halo concentration parameter c(see *), fraction of mass in the disk m_d, and the spin parameter.

There is a lot more in this paper, but they devote a significant section of it to Tully-Fisher relation, explaining the origins of its slope, zeropoint and intrinsic scatter.
- -- slope: They claim that it is a generic prediction of hierarchical structure formation models with CDM-like fluctuation spectra (which set the halo formation times and thus their concentration c distribution).
- -- zeropoint: mostly set on disk mass fraction, mass-to-light radio and the redshift at which a given disk was assembled. They claim that disks must have effectively formed at redshifts close to zero (?), unless we assume an unphysical mass-to-light ratio.
- -- scatter: they analyse possible sources of intrinsic scatter of the disks, and find that:
- --- a small amount of scatter comes from the spin parameter distribution
- --- scatter in concentration c also adds scatter to the TF relation (disks at more concentrated haloes spin faster).
- --- bulge is not included in their model, so bulge luminosity contribution is not accounted for -- that's a source of scatter as well
- --- mass-to-light ratio may vary, adding some more scatter
- --- formation times may vary as well, adding even more scatter.
The intrinsic scatter because of the first two factors cannot be smaller than 0.15 mag.
In conclusion, they show that it is possible to derive a realistic TF relation theoretically, however, I'm not sure if that is the only way it could arise? They do not include bulges, which are important for our sample, too. I am also unsure what do they mean with 'effective disk assembly redshift' at z <= 1.
* c == r_200/r_s, here r_200 -- the limiting radius of a halo, defined so that the mean density inside this radius is 200 times larger than the background density, r_s -- the disk scale length.
There is also a brief explanation of the \sigma_8 parameter -- see attached.

No comments:
Post a Comment