Authors: Dutton, Conroy, van den Bosch et al., http://arxiv.org/abs/1012.5859
Year: 2011
The authors try to find the origins of the TF and Faber-Jackson relations, using a big sample of observed galaxies from SDSS, a set of observational scaling relations showing the distribution of baryons in galaxies, with constrains on the DM halo structure from simulations.
They claim in the introduction that the origin of TFR and FJR is the relation between the halo virial velocity and its virial mass, which scales as v_vir \propto M^(1/3). The relation between v_opt (*) and v_vir depends on 3 factors:
-- the contribution of baryons to v_opt
-- the structure of pristine (DM-only) haloes. The halo profiles are well-enough defined by the NFW profile.
-- and the halo response to the disk formation (contraction/expansion)
The biggest source of uncertainty for the first factor is the IMF, as most of the baryonic mass in galaxies (except the low-mass star-forming ones) is in stars.
The third factor, the halo response, is quite uncertain. It can be adiabatic or non-adiabatic contraction, or expansion due to a number of different processes.
They use a large number of observed relations (TF and FJ relations too) to constrain or predict unknown quantities in their analytic model, modelling the DM halo, bulges, disks, gas disks, constructing 3D models of their SDSS sample galaxies (~100 000 LTGs, ~160 000 ETGs).
They construct mass models for all those galaxies using various IMF and assumptions about the halo response. Then they compare them with the observed circular velocity -- stellar mass relations (I do not understand it at this point -- they already used the TFR as a constraint while solving for the halo contraction at a given IMF, so it is inbuilt in their model somehow?).
Nevertheless, they do not reproduce the zero-point of the TFR with the standard Chabrier IMF and standard adiabatic halo contraction model, as the velocity is overpredicted. They claim that it is possible to fix that by either assuming a different IMF, or changing the halo response, or having different halo concentrations (set by formation time or \sigma_8, they claim that both ways to do it do not solve the zero-point problem).
However, they find that early-type and late-type galaxies cannot have the same IMF and halo response. For any given halo response model, ETGs and LTGs must have different IMF normalisations to reproduce the TFR. If we assume a universal IMF, early-type galaxies require stronger halo contraction.
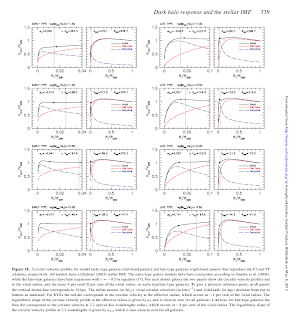They look into the model circular velocity profiles (see attached) for models that reproduce the TF and FJRs, with Chabrier IMF. The velocity profiles look rather constant at higher radii, reaching the maximum at ~0.3 R_vir. (For the LTGs, they convert the velocity dispersion to v_circ picking a rather simple conversion factor between sqrt(2) and sqrt(3).) They claim that the flatness of the rotation curves does not depend strongly on the IMF and the halo response model, and 'is a natural consequence for galaxies embedded in LCDM haloes'.Then they discuss possible mechanisms that would account for differences in IMF or halo response for ETGs and LTGs. The halo contraction/expansion may depend on galaxy morphology via a number of processes:
-- adiabatic contraction due to smooth accretion -- results in disk growth and SF, important for LTGs
-- wet major mergers -- result in halo contraction because gas settles in the center of a galaxy, transforms LTGs to ellipticals
-- dry major mergers ( for ETGs) -- halo contraction due to violent relaxation which mixes stars and DM
-- clumpy accretion/minor mergers: halo expansion due to dynamical friction. Clumps must be baryonic, so that's likely to occur at high redshifts (A. Dekel was arguing in Jerusalem that it must be the case).
-- feedback causes halo expansion, more important to LTGs and for higher redshifts.
-- bars -- halo expansion or contraction, not clear.
They sum it all up by saying that the key formation event that distinguishes ETGs from LTGs is a major merger (dry or wet), which causes halo contraction. For LTGs, haloes could expand due to a combination of clumpy cold accretion and intensive feedback.
The IMF may plausibly vary with redshift due to its alleged dependence on ISM temperature via the Jeans mass. Since ETGs form their stars earlier than LTGs, their IMF might be different. They discuss the van Dokkum & Conroy 2008 article on the different IMF at the cores of massive ellipticals, and conclude that this IMF would not fit for the other ETGs well.
All in all, they show that there is a degeneracy between IMF and the halo response to disk formation, and we cannot match the two for ETGs and LTGs if we want to reproduce the TFR. However, I'm puzzled here -- like in the previous Mo, Mao, White article, they do not model galaxy evolution in a self-contained way, and a model cannot show things that are not included in it. Mo, Mao & White include one set of parameters in their article, and get a set dependences on their parameters (like the disk formation time). Here Dutton et al. model rotation curves as functions of other parameters, and get dependence on another set of parameters. I think it's tricky to understand which parameters are really important, because in astrophysics we often have many coupled parameters, and it's not difficult to find correlations between them. It's more difficult to find out which ones are the fundamental ones, which really affect the TFR.
-- a question: what does it mean "TFR is an edge-on projection of the fundamental plane" (p. 323)?
(*) v2.2 for late-type galaxies and some measure of velocity proportional to dispersion at the effective radius for early types
No comments:
Post a Comment