Python: An Algorithm for Precise Aperture Photometry of Critically Sampled Images

An Algorithm for Precise Aperture Photometry of Critically Sampled Images, Bickerton and Lupton 2013.

lit: Stellar mass-to-light ratios and the Tully-Fisher relation

I'll have to read this when I get more sleep: iopscience.iop.org/0004-637X/550/1/212

talk: assembly bias

I had volunteered to give a presentation on 'Detection of assembly bias' by Wang, Weinmann, de Lucia and Yang. It went pretty well today, here are the slides. It explains the difference between galaxy bias, halo bias and assembly bias. As one of my supervisors puts it, 'not good news'.

A colloquium by S. White

This morning I attended a talk on the Planck results by S. White, who contributed a lot to the current theories of cosmology and structure formation (White and Rees 1978, the NFW paper, etc.).
It was a brilliant talk, here are some things that stuck:
-- the strongest evidence we have for the existence of the dark matter does not come from rotation curves, but from CMB measurements instead!
-- the Planck team was able to do background subtraction very well because they had data from several channels: maps of synchro emission at radio frequencies and dust maps at FIR. Only 3% of the sky had to be interpolated.
-- Planck has the best dust maps of all time due to the previous point.
-- the mass map of the Universe from gravitational lensing measurements is incredible, and strongly correlates with cluster locations from the S-Z effect.
-- the spectral index n of the H-Z spectrum is not equal to 1 (this was news to me, I thought it should be close), but is near 0.96.
-- sigma_8 is less than 1 too (0.83, if I remember correctly)
-- there are issues w/ Planck-WMAP-SPT inter-calibration
-- the CMB is the edge of the visible Universe -- this is obvious, but I hadn't thought of it this way before.
-- there still are anomalies: the cold spot, differences of amount of structure between hemispheres, some structure that is compatible with a rotating Universe

lit: Where do the dwarf galaxies go?

I've just attended a colloquium by J. Navarro of the NFW fame, which was really related to my current reading list. I'm writing an introductory chapter on hierarchical galaxy assembly for my thesis at the moment.
One unsolved problem of LCDM cosmology is the apparent lack of dwarf galaxies: simulations and statistical frameworks (such as EPS) predict that we should see a large number (hundreds) of dwarf galaxies around each bright galaxy such as the Milky Way, but we only know of a dozen. Same with Andromeda.
J. Navarro also showed some puzzling properties of local dwarfs, for example, the fact that their star formation histories are wildly different. Some formed all their gas 10 or so Gyr ago, some had a starburst recently, and some have double-peaked SFH's. He presented the work of his student which could explain it: the CLUES simulation shows that a combination of interaction with the collapsing cosmic web, mergers of dwarfs and reionisation stripping can in principle explain this. Some dwarfs lost their gas simply because they moved too fast through the cosmic web. The remainders of such galaxies may be just too faint for us to see.

lit: NFW halo profile properties, relation to TFR

I've a perhaps naive idea to try to obtain the TFR from the halo-stellar mass distribution. Apparently, that's an old thought, but then they didn't have such good halo-stellar mass relation, 'chewed' by AGN and stellar feedback processes on both ends! That's cool.

Daily Paper #13: the σ_8 parameter, explained!

I'm writing the introduction for my thesis and reading the Book, 'Galaxy Formation and Evolution' by Mo et al. There is a clear and accessible explanation of what the σ_8 parameter really means:
In the linear regime the density field ρ is Gaussian, characterised by the scale-invariant Harrison-Zel'dovich spectrum. It means that the power of a mode P(k) ∝ k^(n - 1), and n = 1. This ensures that the gravitational potential does not diverge neither on small nor on large scales.
In order to fully specify the density field in the early Universe we have to observationally constrain the amplitude of the H-Z spectrum. This amplitude sets the amount of clustering of structure, frequently estimated from the two-point correlation function.
When someone measures σ_8 from galaxy clustering now it means that he or she has calculated the variance (difference from the background density) of galaxy number counts within randomly placed spheres with radius R = 8h^-1 Mpc. For galaxies of Milky Way luminosity the variance is ~= 1, however, such variance decreases sharply if the radii of such spheres approach 30h^-1 Mpc. This means that the Universe is non-homogeneous on small scales, but approaches homogeneity on larger ones.
Note that the cosmological parameter σ_8 and the observed galaxy number variance in spheres of radius 8h^-1 Mpc are not equivalent. The structures we observe today are very far in the non-linear regime.

lit: CDM Models, halo structure and rotation of spirals

References therein might be useful. There is a link to Shu (1982, I think), where it is claimed that Tully-Fisher works if the SB times the mass-to-light ratio squared is constant.

Daily Paper #12 -- The I-Band TF relation for Cluster Galaxies

Title: The I Band Tully-Fisher Relation for Cluster Galaxies: a Template Relation, its Scatter and Bias Corrections.
Authors:Giovanelli, Haynes et al.
Year:1997, http://adsabs.harvard.edu/abs/1997AJ....113...53G
This is a 'classic' Tully Fisher paper, still being cited often. Their TF relation is also widely used as the reference.
It is the seventh paper from a series with the same topic, presenting the corrections done and the TF relation fitting procedure. They use velocity widths and I magnitudes of 784 field and cluster galaxies.
They discuss biases occuring and TF scatter extensively, and there are quite a few enlightening observations. For example, while discussing the total observed scatter, they name three main causes for it:

• Raw measurement errors (inclinations, apparent magnitudes, velocities)
• Uncertainties arising from corrections (extinction, inclination correction for velocities, asymmetric drift correction, turbulence, etc.)
• 'Cosmic scatter' -- velocity disk distortions, disk distortions, photometric asymmetries, variations in mass-to-light ratio, variation in disk-to-bulge-ratio, etc.

I think that's a nice distinction to have in mind.
They discuss the error propagation and relative importance of various error sources. One important, and in retrospect quite obvious fact is that that the relative importance of internal extinction correction errors depends on the inclination and intrinsic rotation velocity of a given galaxy: they are the largest for highly inclined, fast-rotating galaxies. Conversely, velocity errors are the most significant for nearly face-on, slowly rotating galaxies. That might be an interesting plot to show.
They discuss the implications of TF scatter too, citing Franx and de Zeeuw 1992 who claim that TF scatter poses a strong constraint on the ellipticity of the potential in the disk plane. Rix and Zaritsky, 1995 find that departures from disk axisymmetry can contribute as much as ~0.15 mag to the TF scatter (optical observations). Eisenstein and Loeb, 1996 find that the TF scatter due to different formation histories of galaxes can be larger than 0.3 mag in some cosmological scenarios (I remember reading that one: the intrinsic scatter of TF is surely smaller than that, and they try to find out why it is so, there must be some regularising factor at work).
They report a slight TF offset dependence on morphology -- this is of course band dependent. They also discuss a number of bias present, such as incompleteness bias (which they correct by fitting the LF), Malmquist bias, edge-of-catalogue bias, effects of cluster environment (which they find to be negligible).
I do not understand some of the corrections done here, namely, the morphological type correction (they add a term to magnitudes of early type galaxies in order to have a straight line TF relation -- why do they do it? Extinction corrections are likely to be different, and why such a TF relation would be useful?).
The residuals of the TFR can show if there are uncorrected selection effects -- i.e. if there is a dependency of them on inclination. However, I would not want to try to cram all galaxies into the same line, if they are intrinsically different. That'd be losing information, in my opinion.

Daily Paper #11: The Origin of Disks and Spheroids in Simulated Galaxies

Title: The Origin of Disks and Spheroids in Simulated Galaxies
Authors:Sales, Navarro et al.
Year:2012, http://arxiv.org/abs/1112.2220
I picked this article because it challenges the standard idea of galaxy formation I had always been taught: that disks were assembled quite recently in rotating, quiescent haloes, whereas spheroidals are results of mergers (or primordial collapse, as my supervisor pointed out). In other words, current morphology is strongly dependent on the assembly history of the haloes.
They use GIMIC simulations I wrote about to obtain a sizeable sample of Milky Way mass range galaxies. Using a kinematic morphology criterion (\kappa_rot, the fraction of kinetic energy corresponding to the ordered rotation, they look for the origin of morphology of a given galaxy. Simulations show that disks can be formed in haloes of high and low spin parameter (Bullock 2001), in haloes that collapse early or late, in haloes that go through merger events.
They find that disks are preferably formed by slow accretion of gas from a hot corona, as opposed to cold flows (many people in Jerusalem claimed those were important at high redshift). Disks assemble slowly and gradually (see fig.6: A galaxy is a spheroid, D galaxy is a disk, BC -- intermediate steps), and hot corona gas accretion might explain that.
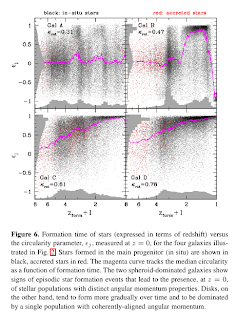Gas accretion history is not the whole story. The authors claim that spin alignment of the accreted gas and the galaxy itself is more important: disks form when the two spin directions are similar, whereas spheroidals form when they are misaligned. Hot corona gas spends a lot of time inside the halo, it is forced to align its rotation with that of the halo and the galaxy itself. Spheroids form when a galaxy accretes a lot of cold gas via misaligned filaments, i.e. when the angular momenta of the galaxy and the gas are not aligned. Star formation in spheroidals proceeds in a bursty manner (due to a different channel of gas acquisition, not the slow and gradual corona gas accretion), leaving behind stars with different ages and angular momenta. Intermediate galaxies form when the spins are aligned, but the gas accreted is mostly cold.
The kinematic (at least) morphology is determined by the interplay of these two factors: in order to form a disk, a galaxy needs to have a lot of shock-heated gas in its corona, unless the spin misalignment between the spins the galaxy and the gas is too large. That may be only a part of the whole picture, as mergers may play a more important role in other mass ranges, they mention halo triaxiality and feedback as other potential factors of morphology. I think it is an interesting article, even if not directly related to TF. It reasserts what I had repeatedly heard in Jerusalem: that inflows and outflows are very important, and we do not know much about them. The results may be tested observationally: would it be possible to do something like fig.6 with CALIFA data?

Python: splitting a list into a number of roughly equal chunks

I used this solution, however, since I wanted to have a set number of chunks as opposed to chunks of a set length, the function ended up being slightly different:

def splitList(longList, chunkNumber):
    #Get the number of elements in a chunk we want
    n = int(math.floor(len(longList)/chunkNumber)) + 1
    print n, 'length of a chunk'
    return [longList[i:i+n] for i in range(0, len(longList), n)]

LaTeX: draft class

Yesterday, while doing some unrelated stuff, I found out that it is useful to put \documentclass[a4paper][draft]{article} into the preamble sometimes, this shows the blocks of the document and can be really helpful if the layout is messed up.