lit: Angular momentum and galaxy formation revisited

Romanowsky and Fall 2012 -- See the discussion of mass and angular momentum as the main parameters for galaxies, also the appendix for deprojection.

lit: Galaxies in LCDM with halo abundance matching

Trujillo-Gomez et al. 2011 -- Bolshoi resimulation also reproduces M-v_c relation.

lit: The Zeldovich approximation: key to understanding Cosmic Web complexity

Hidding, Shandarin et al. 2013: seems interesting, modelling the structure of the cosmic web.

Python: scikit-learn MoG

Probably should have tried this, before reinventing the wheel.

MCMC -- how to sample a multi-modal Gaussian

see this.

lit: Verheijen et al, volume complete TFR, also declining rotation curves

see Verheijen et al. article on a volume-complete TF sample.
Also, the references therein, esp. Casertano & Van Gorkom, 1991 for a discussion of declining rotation curves in more massive galaxies.

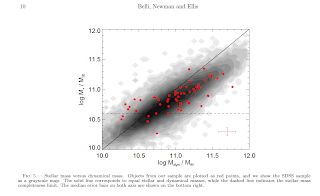
lit: Velocity dispersions and dynamical masses for a large sample of quiescent galaxies at z>1

By Belli et al. They show that the stellar-dynamical mass ratio for massive ellipticals was in place at z > 1.

lit: Yegorova et al. 2007

A detailed investigation of the dependence of the slope of TFR on the radius where the velocity is measured. They find that the scatter is smallest at R = 0.6 R_opt (see fig.5).

lit: Some aspects of measurement error in linear regression of astronomical data, Kelly 2007

Kelly 2007:
I describe a Bayesian method to account for measurement errors in linear regression of astronomical data. The method allows for heteroscedastic and possibly correlated measurement errors and intrinsic scatter in the regression relationship. The method is based on deriving a likelihood function for the measured data, and I focus on the case when the intrinsic distribution of the independent variables can be approximated using a mixture of Gaussian functions. I generalize the method to incorporate multiple independent variables, non-detections, and selection effects (e.g., Malmquist bias).

LaTeX: \include vs. \input

I was annoyed by a page break that appears if I \include{a portion of my document}. Using \input{} instead solves this.

lit: Tonini et al. 2013, on physically meaningful radius for velocity measurements

They define the 'corrected' disk scale-length that includes the bulge potential. Pay attention to this article anyway -- they add a dynamical classificator dimension to the TFR, which is a little bit akin to what I'm doing.

Daily paper: The Tully-Fisher relations of early-type spiral and S0 galaxies

I gave a talk at our group meeting yesterday, this was one of several useful suggestions and references I got. bWilliams et al. 2010, The Tully-Fisher relations of early-type spiral and S0 galaxies
Offsets which are ascribed to fading or brightening could in fact be due to systematic biases that differ between the measures of rotation used. For typical slopes of the TFR, a relatively small systematic difference in velocity of ∼0.1 dex introduces an offset in the TFR that is indistinguishable from a ∼ 1mag difference in luminosity.
Our conclusions in this section have three consequences for previous works that measure the TFR of S0 galaxies using stellar kinematics corrected for asymmetric drift (e.g. Neistein et al. 1999; Hinz et al. 2001, 2003, BAM06): (i) the asymmetric drift correction they use yields similar results to detailed Jeans modelling; (ii) the drift correction does not seem to introduce a systematic bias between spirals and S0s and, if applied to samples of both spirals and S0s, can indeed be used to compare the TFRs of the two classes; (iii) however, a TFR derived from asymmetric drift-corrected stellar kinematics cannot be directly compared to TFRs derived from global HI line widths or resolved emission line PVDs. ==== There's a really interesting section on the ADC, and a nice comparison of gas/HI/AD corrected stellar kinematics. Also I should check their section on TFR fitting, intrinsic scatter in it, etc.In addition, I ought to take a look at the references therein, esp. the introduction.

SQLITE: nested query for MoG

select avg(gc.r_mag) from luminosity_errors2 as gc where gc.califa_id in(select t.califa_id from tidal_influence as t where t.Ftop > -0 and t.Ftop <98)

lit: Kassin 2007

Check it for unordered rotation corrections

lit: Face-on TFR with IFU

Andersen and Bershady 2003

lit: TFR at z=2.2 with SINFONI IFU

Cresci et al. 2013 -- they also use genetic algorithms for velocity field modelling.

lit: The power spectrum dependence of dark matter halo concentrations

Eke et al. 2001

lit: The baryonic Tully–Fisher relation and galactic outflows

Dutton and van den Bosch 2009, also see Dutton et al. 2011.

lit: testing CDM with low-mass TFR

Blanton et al. 2008.

lit: The baryonic Tully-Fisher relation and its implication for dark matter halos

Trachternach et al 2009: baryonic TFR as constraint of elongation of DM haloes.

lit: IFU observations of galaxies wrt TFR

Courteau 2003 is important: they observe 14 barred galaxies with Sparse Pak IFU in order to calibrate long-slit samples. To be discussed in talk/article!

lit: Skewness and kurtosis in BTFR

McGaugh 2012:
A persistent problem with interpreting astronomical data is whether Gaussian statistics actually apply. One reason for this is that systematic errors often dominate random ones. We can check whether this might be an issue here by examining higher order statistics like the skew (lopsidedness) and kurtosis (pointiness) of the distribution in the deviations perpendicular to the BTFR. If the data are well behaved (i.e., distributed normally), the skew and kurtosis should be small.

The difference between MCMC and simulations

from PSU astrostatistics lecture notes:
MCMC is a form of simulation, because MCMC generates random numbers and bases the inference on them. However, there are two important differences between MCMC and the simulation that we shall discuss here.
a) In MCMC we do not simulate from the target distribution directly. Instead, we simulate a Markov Chain that converges to the target distribution. Thus, MCMC performs approximate simulation.
b) The primary use of MCMC is in Bayesian statistics where we seek to simulate from the posterior distribution of the parameters. Classical simulation on the other hand simulates fresh data.